Así es como los estudiantes del pequeño país asiático resuelven un problema de matemáticas

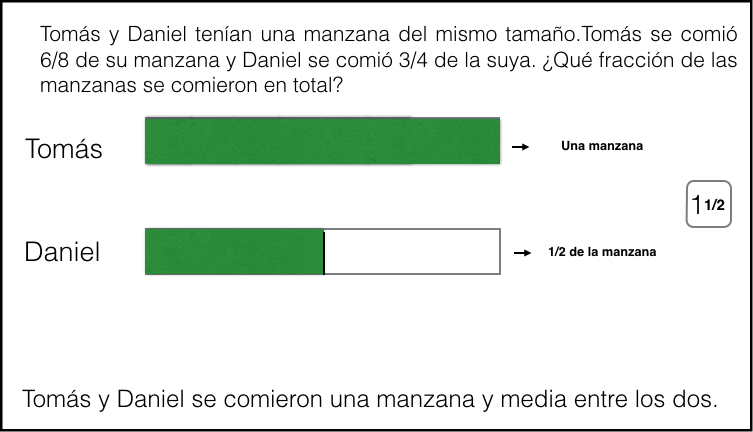
Tomás y Daniel tenían una manzana del mismo tamaño. Tomás se comió 6/8 de su manzana y Daniel se comió 3/4 de la suya. ¿Qué fracción de manzanas se comieron en total?

Algún matemático podría dar la respuesta y ejemplificar la forma tradicional de resolver este ejercicio. Sin embargo, de acuerdo a la metodología de Singapur, nunca hay sólo una forma de llegar a la respuesta. En cada problema hay al menos dos maneras, dos vías de llegar a una solución, que en general están relacionadas con distintas formas de comprensión.

En el modelo de barras un niño resolvería este problema del siguiente modo.

1. En la historia participan dos personas, Tomás y Daniel, que tenían una manzana del mismo tamaño.

 

2. Tomás se comió 6/8 de su manzana. Por lo tanto, el niño divide la manzana en 8 partes iguales y representa las 6 partes que Tomás se comió de esas ocho.

3. Daniel se comió 3/4 de la suya, así que partimos la misma manzana en 4 partes y representamos las 3 partes que se come de esas 4.

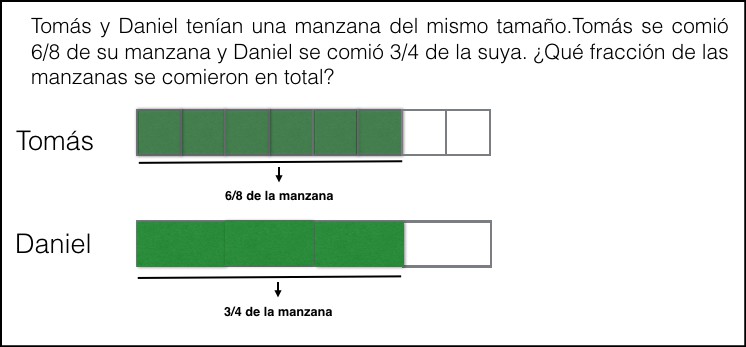
Con esta información, ¿podemos responder la pregunta? Todavía no, porque la pregunta es qué fracción de las manzanas se comieron en total ambos. Y el problema es que Tomás tiene una manzana dividida en 8 y Daniel otra dividida en 4.

Si respondiéramos que se comieron en total 9 partes las dos manzanas no sería una respuesta precisa, porque entonces podríamos decir, por ejemplo, que si Tomás se comió 9 y Daniel 3, entonces Tomás comió más que Daniel, lo cual no es correcto.

4. ¿Cómo podríamos hacer? Si son manzanas del mismo tamaño, también podríamos dividir en 8 la manzana de Daniel, y entonces podríamos ver más fácil visualmente que Daniel se comió también 6/8 de la manzana.

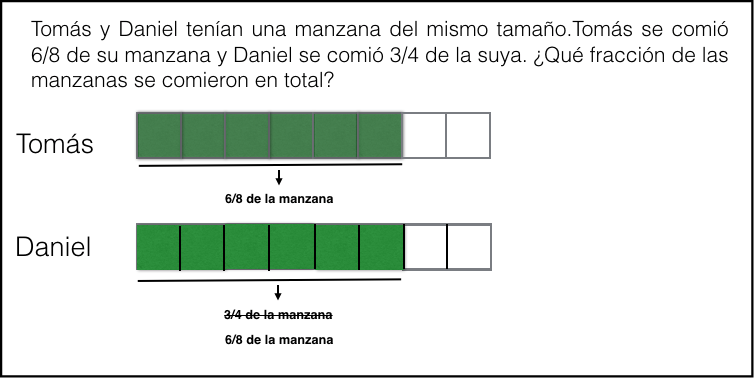
5. Ahora sí que pueden relacionar los 6/8 de Tomás y los 6/8 de Daniel, y decir que podemos tomar algo de lo que se comió Daniel y añadirlo a lo que se comió Tomás.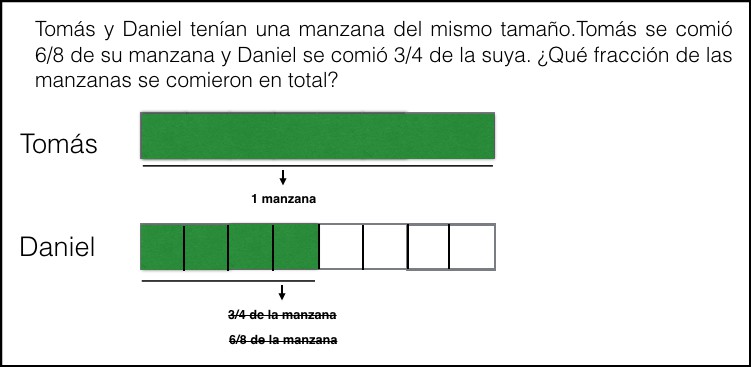

6. Podríamos concluir que Tomás y Daniel como mínimo se comieron una manzana. Es importante que el niño vea que no es que Tomás se comió una manzana, sino que entre los dos se comieron al menos una manzana.

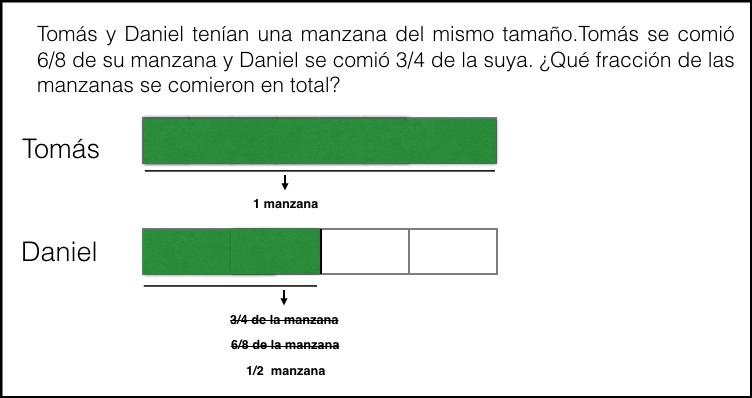
7. A Daniel le queda ahora media manzana y por tanto podemos concluir que Tomás y Daniel se comieron entre los dos 1 manzana y media. Es importante que el niño vea que no es que Tomás se comió una manzana y Daniel media, sino que entre los dos se comieron una manzana y media. Lo representarlo visualmente de este otro modo.

Si el niño no es capaz de expresar la respuesta correcta, debemos volver sobre el proceso visual para comprender el pensamiento que le ha llevado a dar con otro resultado.